Beschrijving van de optimale cyclus

Elke beweging gebeurt in 3 fasen: eenparige versnelling, constante snelheid en weer eenparige versnelling tot het stil staat. De versnellingen zijn tegengesteld, en nemen dus evenveel tijd in beslag (ook dezelfde afstand).

Voor eenparige versnelling geldt:

$$v = a \cdot t_v$$

En dus:

$$t_v = \frac{v}a$$

Bij deze fase is de afgelegde weg:

$$x_v = \frac{a\cdot t_v^2}2 = \frac{v^2}{2a}$$

Voor constante snelheid geldt:

$$x_c = v \cdot t_c$$

En dus:

$$t_c = \frac{x_c}v = \frac{x - 2x_v}v = \frac{x}v - \frac{v}a$$

De totale tijd nodig voor deze beweging is dus:

$$t_{tot} = 2t_v + t_c = \frac va + \frac xv$$ (1)

Voor rotatie geldt dan:

$$t_{tot} = \frac\omega\alpha + \frac\theta\omega$$ (2)

Er zijn twee mogelijkheden voor de eindsituatie: ofwel de knik naar rechts (a), ofwel de knik naar links (b), waarbij resp. de tweede motor het meeste werk heeft, resp. de eerste. De beweging waarbij een van de motoren het langst moet werken zal uiteraard de minst efficiëntste zijn. Daarvoor worden eerst de begin- en eindpositie berekend (via sinus- en cosinusregels):

$$\begin{eqnarray*} \beta_{1\phantom b} = 0.8845 & \qquad & \gamma_{1\phantom b} ... ...96 \\ \beta_{2b} = 2.3197 & \qquad & \gamma_{2b} = -1.6297 \\ \end{eqnarray*}$$

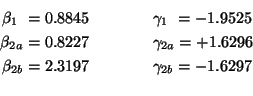
Met formule worden de minimale tijden berekend voor elke beweging. Voor de knik rechts:

$$t_{\beta a} = 0.1045 \qquad t_{\gamma a} = 0.2731$$

Voor de knik links:

$$t_{\beta b} = 0.1765 \qquad t_{\gamma b} = 0.0702$$

Hieruit volgt dat er minder tijd nodig is om te komen tot de situatie b.